Evaluation¶
Given a dataset of items where a user has implicitly or explicitly interacted with (via ratings, purchases, downloads, previews, etc.), the idea is to split the dataset in two—usually disjunct—sets. The training and test datasets.
The evaluation package implements several metrics such as: predictive accuracy (Mean Absolute Error, Root Mean Square Error), decision based (Precision, Recall, F–measure), and rank based metrics (Spearman’s 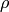 , Kendall–
, Kendall–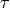 , and Mean Reciprocal Rank)
, and Mean Reciprocal Rank)
For a complete list of available metrics to evaluate recommender systems see [http://research.microsoft.com/pubs/115396/EvaluationMetrics.TR.pdf]
Given a test set 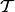 of user-item pairs
of user-item pairs 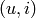 with ratings
with ratings 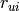 , the system generates predicted ratings
, the system generates predicted ratings 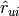 .
.
Prediction-based metrics¶
Predictive metrics aim at comparing the predicted values against the actual values. The result is the average over the deviations.
Mean Absolute Error¶
[http://en.wikipedia.org/wiki/Mean_absolute_error]
Mean Absolute Error (MAE) measures the deviation between the predicted and the real value:
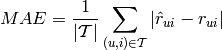
where 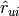 is the predicted value of user
is the predicted value of user  for item
for item 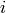 , and
, and 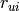 is the true value (ground truth).
is the true value (ground truth).
Examples¶
from recsys.evaluation.prediction import MAE
mae = MAE()
mae.compute(4.0, 3.2) #returns 0.8
from recsys.evaluation.prediction import MAE
DATA_PRED = [(3, 2.3), (1, 0.9), (5, 4.9), (2, 0.9), (3, 1.5)]
mae = MAE(DATA_PRED)
mae.compute() #returns 0.7
from recsys.evaluation.prediction import MAE
GROUND_TRUTH = [3.0, 1.0, 5.0, 2.0, 3.0]
TEST = [2.3, 0.9, 4.9, 0.9, 1.5]
mae = MAE()
mae.load_ground_truth(GROUND_TRUTH)
mae.load_test(TEST)
mae.compute() #returns 0.7
Root Mean Squared Error¶
[http://en.wikipedia.org/wiki/Root_mean_square_deviation]
Mean Squared Error (MSE) is also used to compare the predicted value with the real value a user has assigned to an item. The difference between MAE and MSE is that MSE heavily penalise large errors.
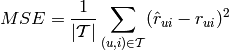
Root Mean Squared Error (RMSE) equals to the square root of the MSE value.
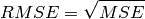
Examples¶
from recsys.evaluation.prediction import RMSE
rmse = RMSE()
rmse.compute(4.0, 3.2) #returns 0.8
from recsys.evaluation.prediction import RMSE
DATA_PRED = [(3, 2.3), (1, 0.9), (5, 4.9), (2, 0.9), (3, 1.5)]
rmse = RMSE(DATA_PRED)
rmse.compute() #returns 0.891067
Decision-based metrics¶
Decision-based metrics evaluates the top-N recommendations for a user. Uusally recommendations are a ranked list of items, ordered by decreasing relevance. Yet, the decision-based metrics do not take into account the position -or rank- of the item in the result list).
There are four different cases to take into account:
- True positive (TP). The system recommends an item the user is interested in.
- False positive (FP). The system recommends an item the user is not interested in.
- True negative (TN). The system does not recommend an item the user is not interested in.
- False negative (FN). The system does not recommend an item the user is interested in.
| Relevant | Not relevant | |
| Recommended | TP | FP |
| Not recommended | FN | TN |
Precision (P) and recall (R) are obtained from the 2x2 contingency table (or confusion matrix) shown in the previous Table.
Precision¶
[http://en.wikipedia.org/wiki/Precision_and_recall]
Precision measures the fraction of relevant items over the recommended ones.
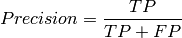
Precision can also be evaluated at a given cut-off rank, considering only the top–n recommendations. This measure is called precision–at–n or P@n.
When evaluating the top–n results of a recommender system, it is quite common to use this measure:
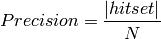
where 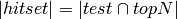 .
.
Recall¶
Recall measures the coverage of the recommended items, and is defined as:

Again, when evaluating the top–N results of a recommender system, one can use this measure:
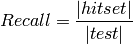
F-measure¶
[http://en.wikipedia.org/wiki/F1_score]
F–measure combines P and R results, using the weighted harmonic mean.
The general formula (for a non-negative real 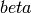 value) is:
value) is:
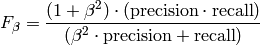
Two common F–measures are 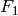 and
and 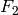 .
In
.
In 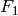 recall and precision are evenly weighted, whilst
recall and precision are evenly weighted, whilst 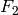 weights recall twice as much as precision.
weights recall twice as much as precision.
Example¶
from recsys.evaluation.decision import PrecisionRecallF1
TEST_DECISION = ['classical', 'invented', 'baroque', 'instrumental']
GT_DECISION = ['classical', 'instrumental', 'piano', 'baroque']
decision = PrecisionRecallF1()
decision.load(GT_DECISION, TEST_DECISION)
decision.compute() # returns (0.75, 0.75, 0.75)
# P = 3/4 (there's the 'invented' result)
# R = 3/4 ('piano' is missing)
The main drawback of the decision–based metrics is that do not take into account the ranking of the recommended items. Thus, an item at top–1 has the same relevance as an item at top–20. To avoid this limitation, we can use rank–based metrics.
Rank-based metrics¶
Spearman’s rho¶
[http://en.wikipedia.org/wiki/Spearman’s_rank_correlation_coefficient]
Spearman’s 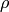 computes the rank–based Pearson correlation of two ranked lists.
It compares the predicted list with the user preferences (e.g. the ground truth data), and it is defined as:
computes the rank–based Pearson correlation of two ranked lists.
It compares the predicted list with the user preferences (e.g. the ground truth data), and it is defined as:
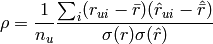
Examples¶
Using explicit ranking information:
from recsys.evaluation.ranking import SpearmanRho
TEST_RANKING = [('classical', 25.0), ('piano', 75.0), ('baroque', 50.0), ('instrumental', 25.0)]
GT_RANKING = [('classical', 50.0), ('piano', 100.0), ('baroque', 25.0), ('instrumental', 25.0)]
spearman = SpearmanRho()
spearman.load(GT_RANKING, TEST_RANKING)
spearman.compute() #returns 0.5
Rank-based correlation for ratings:
from recsys.evaluation.ranking import SpearmanRho
DATA_PRED = [(3, 2.3), (1, 0.9), (5, 4.9), (2, 0.9), (3, 1.5)]
spearman = SpearmanRho(DATA_PRED)
spearman.compute() #returns 0.947368
Kendall–tau¶
[http://en.wikipedia.org/wiki/Kendall_tau_rank_correlation_coefficient]
Kendall–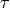 also compares the recommended (
also compares the recommended (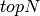 ) list with the user’s preferred list of items.
Kendall–
) list with the user’s preferred list of items.
Kendall–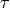 rank correlation coefficient is defined as:
rank correlation coefficient is defined as:

where  is the number of concordant pairs, and
is the number of concordant pairs, and 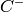 is the number of discordant pairs in the data set.
is the number of discordant pairs in the data set.
Examples¶
Using explicit ranking information:
from recsys.evaluation.ranking import KendallTau
TEST_RANKING = [('classical', 25.0), ('piano', 75.0), ('baroque', 50.0), ('instrumental', 25.0)]
GT_RANKING = [('classical', 50.0), ('piano', 100.0), ('baroque', 25.0), ('instrumental', 25.0)]
kendall = KendallTau()
kendall.load(GT_RANKING, TEST_RANKING)
kendall.compute() #returns 0.4
Rank-based correlation for ratings:
from recsys.evaluation.ranking import KendallTau
DATA_PRED = [(3, 2.3), (1, 0.9), (5, 4.9), (2, 0.9), (3, 1.5)]
kendall = KendallTau(DATA_PRED)
kendall.compute() #returns 0.888889
Mean reciprocal Rank¶
[http://en.wikipedia.org/wiki/Mean_reciprocal_rank]
Mean Reciprocal Rank (MRR) is defined as:

Recommendations that occur earlier in the top–n list are weighted higher than those that occur later in the list.
Example¶
Computing reciprocal rank (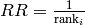 ) for one query:
) for one query:
from recsys.evaluation.ranking import ReciprocalRank
GT_DECISION = ['classical', 'instrumental', 'piano', 'baroque']
QUERY = 'instrumental'
rr = ReciprocalRank()
rr.compute(GT_DECISION, QUERY) #returns 0.5 (1/2): found at position (rank) 2
Mean reciprocal rank for a list of queries 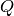 :
:
from random import shuffle
from recsys.evaluation.ranking import MeanReciprocalRank
TEST_DECISION = ['classical', 'invented', 'baroque', 'instrumental']
GT_DECISION = ['classical', 'instrumental', 'piano', 'baroque']
mrr = MeanReciprocalRank()
for QUERY in TEST_DECISION:
shuffle(GT_DECISION) #Just to "generate" a different GT each time...
mrr.load(GT_DECISION, QUERY)
mrr.compute() #in my case, returned 0.45832
Mean Average Precision¶
[http://en.wikipedia.org/wiki/Mean_average_precision]
Mean Average Precision (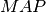 ) is defined as:
) is defined as:
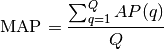
where 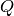 is the number of queries, and
is the number of queries, and 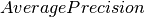 (AP) [http://en.wikipedia.org/wiki/Mean_average_precision#Average_precision] equals:
(AP) [http://en.wikipedia.org/wiki/Mean_average_precision#Average_precision] equals:

where 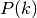 is Precision at top-k, and
is Precision at top-k, and  is an indicator function equaling 1 if the item at rank is a relevant document, and zero otherwise.
is an indicator function equaling 1 if the item at rank is a relevant document, and zero otherwise.
Recommendations that occur earlier in the top–n list are weighted higher than those that occur later in the list.
Example¶
Computing average Precision (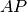 ) for one query,
) for one query, 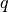 :
:
from recsys.evaluation.ranking import AveragePrecision
ap = AveragePrecision()
GT = [1,2,3,4,5]
q = [1,3,5]
ap.load(GT, q)
ap.compute() # returns 1.0
GT = [1,2,3,4,5]
q = [99,3,5]
ap.load(GT, q)
ap.compute() # returns 0.5833335
Mean Average Precision for a list of retrieved results 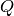 :
:
from recsys.evaluation.ranking import MeanAveragePrecision
GT = [1,2,3,4,5]
Q = [[1,3,5], [99,3,5], [3,99,1]]
Map = MeanAveragePrecision()
for q in Q:
Map.load(GT, q)
Map.compute() # returns 0.805556