Algorithms

pyrecsys provides, out of the box, some basic algorithms based on matrix factorization.

SVD

pyrecsys makes use of SVD in order to decompose the input data (a matrix). Once the matrix is reduced into a lower dimensional space, pyrecsys can provide predictions, recommendations and similarity among the “elements” (being either users or items -it’s just a matter of how you load the matrix data-).

Loading data

How to load a dataset (e.g. Movielens 10M)?

from recsys.algorithm.factorize import SVD

filename = './data/movielens/ratings.dat'
svd = SVD()
svd.load_data(filename=filename, sep='::', format={'col':0, 'row':1, 'value':2, 'ids': int})
    # About format parameter:
    #   'row': 1 -> Rows in matrix come from second column in ratings.dat file
    #   'col': 0 -> Cols in matrix come from first column in ratings.dat file
    #   'value': 2 -> Values (Mij) in matrix come from third column in ratings.dat file
    #   'ids': int -> Ids (row and col ids) are integers (not strings)

Split a dataset (train and test):

from recsys.datamodel.data import Data
from recsys.algorithm.factorize import SVD

filename = './data/movielens/ratings.dat'
data = Data()
format = {'col':0, 'row':1, 'value':2, 'ids': int}
data.load(filename, sep='::', format=format)
train, test = data.split_train_test(percent=80) # 80% train, 20% test

svd = SVD()
svd.set_data(train)

Loading a file, executing external SVDLIBC program, and creating an SVD instance svd:

from recsys.utils.svdlibc import SVDLIBC
svdlibc = SVDLIBC('./data/movielens/ratings.dat')
svdlibc.to_sparse_matrix(sep='::', format={'col':0, 'row':1, 'value':2, 'ids': int}) # Convert to sparse matrix format [http://tedlab.mit.edu/~dr/SVDLIBC/SVD_F_ST.html]
svdlibc.compute(k=100)
svd = svdlibc.export()

Computing

>>> K=100
>>> svd.compute(k=K, min_values=10, pre_normalize=None, mean_center=True, post_normalize=True, savefile=None)

Parameters:

min_values: remove those rows or columns (from the input matrix) that has less than ‘min_values’ non-zeros

pre_normalize: normalize input matrix. Possible values are tfidf, rows, cols, all.

tfidf: By default, treats the matrix as terms-by-documents. It’s important, then, how the data is loaded. Use the format param in svd.load_data() to determine the order of the fields of the input file.

rows: Rescales the rows of the input matrix so that they all have unit Euclidean magnitude

cols: Rescales the columns of the input matrix so that they all have unit Euclidean magnitude

all: Rescales the rows and columns of the input matrix, by dividing both the rows and the columns by the square root of their Euclidean norm

mean_center: centering the input matrix (aka mean substraction)

post_normalize: Normalize every row of to be a unit vector. Thus, row similarity (using cosine distance) returns

savefile: Output file to store SVD transformation ( vectors)

Predictions

To predict a rating, 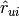, SVD class reconstructs the original matrix,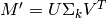

Then,

>>> svd.predict(ITEMID, USERID, MIN_RATING=0.0, MAX_RATING=5.0)

equals to:

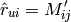
Here are the RMSE and MAE values for the Movielens 10M dataset (Train: 8,000,043 ratings, and Test: 2,000,011), using 5-fold cross validation, and different K values or factors (10, 20, 50, and 100) for SVD:

K	10	20	50	100
RMSE	0.87224	0.86774	0.86557	0.86628
MAE	0.67114	0.66719	0.66484	0.66513

Recommendations

Recommendations (i.e. unknown values in 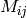) are also derived from 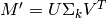. In this case,

>>> svd.recommend(USERID, n=10, only_unknowns=True, is_row=False)

returns the higher values (e.g. items that the user has not rated) of 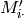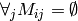, whilst

>>> svd.recommend(USERID, n=10, only_unknowns=False, is_row=False)

returns the best items for the user

Neighbourhood SVD

Classic Neighbourhood algorithm uses the ratings of the similar users (or items) to predict the values of the input matrix M.

from recsys.algorithm.factorize import SVDNeighbourhood

svd = SVDNeighbourhood()
svd.load_data(filename=sys.argv[1], sep='::', format={'col':0, 'row':1, 'value':2, 'ids': int})
K=100
svd.compute(k=K, min_values=5, pre_normalize=None, mean_center=True, post_normalize=True)

Predictions

The only difference with plain SVD is the way how it computes the predictions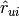

>>> svd.predict(ITEMID, USERID, weighted=True, MIN_VALUE=0.0, MAX_VALUE=5.0)

To compute the prediction, it uses this equation (u=USERID, i=ITEMID):

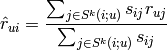
where

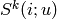denotes the set of 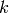items rated by , which are most similar to .

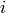• To compute the 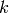items most similar to 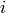, it uses the svd.similar(i) method. Then it gets those items that user has already rated

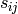is the similarity between 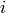and 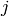, computed using svd.similarity(i, j)

Comparison

For those who love RMSE, MAE and the like, here are some numbers comparing both SVD approaches. The evaluation uses the Movielens 1M ratings dataset, splitting the train/test dataset with ~80%-20%.

Note

Computing svd k=100, min_values=5, pre_normalize=None, mean_center=True, post_normalize=True

Warning

Because of min_values=5, some rows (movies) or columns (users) in the input matrix are removed. In fact, those movies that had less than 5 users who rated it, and those users that rated less than 5 movies are removed.

Results

Movielens 1M dataset (number of ratings in the Test dataset: 209,908):

	SVD	SVD Neigh.
RMSE	0.91811	0.875496
MAE	0.71703	0.684173